Vectorizing Time with Time2Vec
Published on
Introduction
Machine Learning models can only understand data that can be encoded in a numerical form.
Real Numbers such as Distances, Mass, Population, etc. can be simply normalized and fed to a Machine Learning Algorithm. Here’s a list of “type” of Data and most “standard” way of encoding them (pun intended).
| Data Type | Encoding Method |
|---|---|
| Numerical - Ratio | Normalize |
| Numerical - Interval | Normalize/Label + One-Hot Encode |
| Categorical - Ordinal/Nominal | Label + One-Hot Encode |
| Images | Normalize Across Channels |
| Words | Label + One-Hot Encode |
| Graphs | Edge Index + Node Features |
But things aren’t so straight forward for some type of data.
For example, how would you encode a Date? Traditionally, only features extracted from Dates have been used, such as “Weekend/Weekday”, “Season”, “Quarter” etc, as one would notice, that this would lead to a lot of information loss, how do we encapsulate the entire information in a given date?
Consider a date 2021-01-12, Should we normalize across Year, Month, and Day as separate features? or One-Hot encode them? Why is this a bad idea?
- Periodicity of Days, Months, and Years is not captured by neural nets with non-periodic activation functions (Most neural nets).
- Exploding/Vanishing Gradients due to growing inputs.
Time2Vec
Say \(\tau\ \in \mathbb{R}^d\) is a periodic input variable for which we want to learn a vector representation \(v \in \mathbb{R}^{k}\).The Time2Vec “Layer” is defined as:
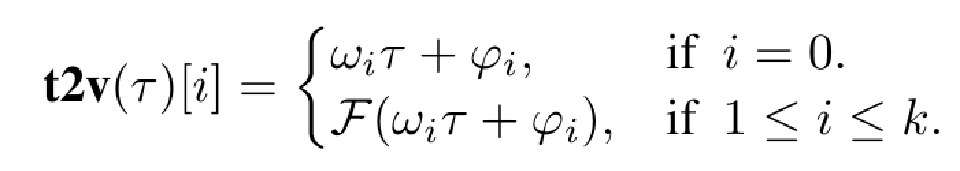
Where,
- \(\cal F\) is a periodic function for e.g. \(Sine(\sdot)\) or \(Cosine(\sdot)\)
- \(w_i, \varphi_{i}\) are learnable parameters
Points to Note:
- \(k-1\) components learn periodic features, \(1 \le i \le k\).
- One component allows learning of Non-periodic features, \(i = 0\).
Link to the Paper: “Time2Vec: Learning a Vector Representation of Time”
Time2Vec - Code
We’ll use PyTorrch with my open-source implementation of Time2Vec here
PyTorch implementation
import torch
from torch import nn
import numpy as np
import math
def t2v(tau, f, out_features, w, b, w0, b0):
# k-1 periodic features
v1 = f(torch.matmul(tau, w) + b)
# One Non-periodic feature
v2 = torch.matmul(tau, w0) + b0
return torch.cat([v1, v2], 1)
class SineActivation(nn.Module):
def __init__(self, in_features, out_features):
super(SineActivation, self).__init__()
self.out_features = out_features
self.w0 = nn.parameter.Parameter(torch.randn(in_features, 1))
self.b0 = nn.parameter.Parameter(torch.randn(in_features, 1))
self.w = nn.parameter.Parameter(torch.randn(in_features, out_features-1))
self.b = nn.parameter.Parameter(torch.randn(in_features, out_features-1))
self.f = torch.sin
def forward(self, tau):
return t2v(tau, self.f, self.out_features, self.w, self.b, self.w0, self.b0)
I think the code is self-explanatory.
I have also provided a pretrained model to encode Date-Time in ISO format (e.g. 13:23:30 2019-7-23) to a vector of 64 dimensions. The pretraining task is “Next Date Prediction”, a dataset of pairs of date-time and their immediate next date-time is generated and trained in a supervised fashion. After training, the decoder is discarded, and it can be now used to generate embeddings for date-time.
A sample code for getting embedding from this Date2Vec package is shown below.
from Model import Date2VecConvert
import torch
# Date2Vec embedder object
# Loads a pretrained model
d2v = Date2VecConvert(model_path="./d2v_model/d2v_98291_17.169918439404636.pth")
# Date-Time is 13:23:30 2019-7-23
x = torch.Tensor([[13, 23, 30, 2019, 7, 23]]).float()
# Get embeddings
embed = d2v(x)
print(embed, embed.shape)
Conclusion
We talked about an incredibly simple technique that allows Neural Nets to understand periodic features.